9. Normalization example

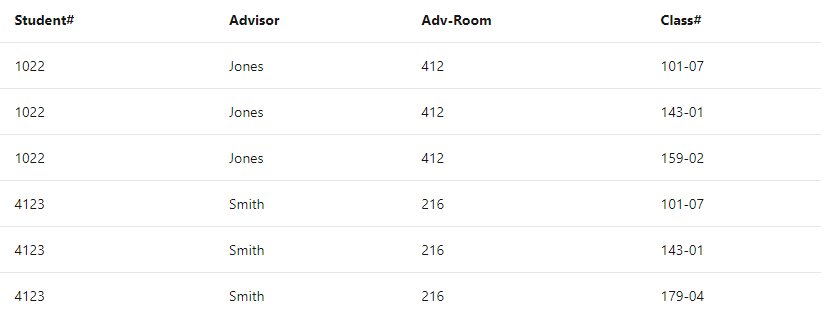
Here is an unnormalized table:

First normal form: No repeating groups

Tables should have only two dimensions. Since one student has several classes, these classes should be listed in a separate table. Fields Class1, Class2, and Class3 in the above records are indications of design trouble.

Spreadsheets often use the third dimension, but tables should not. Another way to look at this problem is with a one-to-many relationship, do not put the one side and the many side in the same table. Instead, create another table in first normal form by eliminating the repeating group (Class#), as shown below:

Second normal form: Eliminate redundant data

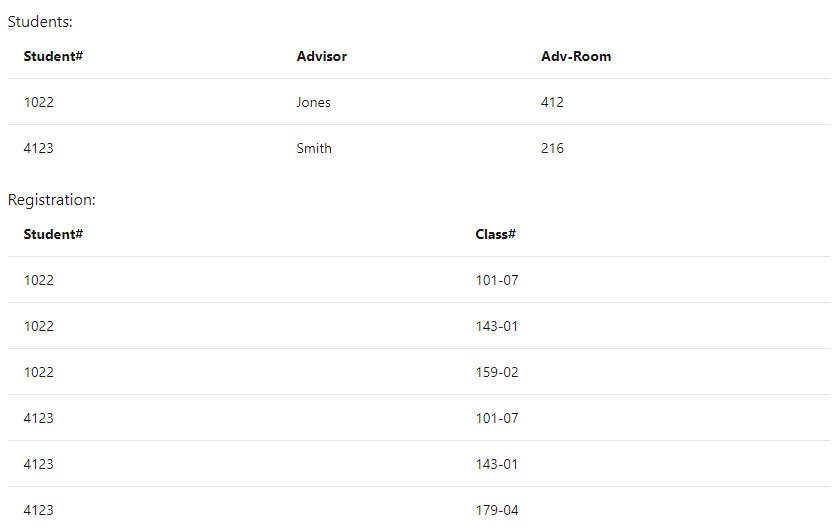
Note the multiple Class# values for each Student# value in the above table. Class# is not functionally dependent on Student# (primary key), so this relationship is not in second normal form.

The following tables demonstrate second normal form:

Third normal form: Eliminate data not dependent on the primary key (Student#).

Every non-primary key attribute is non-transitively dependent on the primary key.

In the last example, Adv-Room (the advisor’s office number) is functionally dependent on the Advisor attribute. The solution is to move that attribute from the Students table to the Faculty table, as shown below:

Also:

Boyce-Codd normal form (BCNF)

Table is in 3NF. All non-trivial functional dependencies depend on a super key.

Fourth Normal Form (4NF)

Table is in 3NF. For every muti-value dependency A -> B, A is a candidate key.

Let’s use this table as an example:

A super key is a set of one or more attributes (columns), which can uniquely identify a row in a table.

Super keys in this table are:

• {Emp_SSN}
• {Emp_Number}
• {Emp_SSN, Emp_Number}
• {Emp_SSN, Emp_Name}
• {Emp_Number, Emp_Name}
• {Emp_SSN, Emp_Number, Emp_Name}

A candidate key is a minimal super key with no redundant attributes. The following two set of super keys are chosen from the above sets as there are no redundant attributes in these sets.

• {Emp_SSN}
• {Emp_Number}

Only these two sets are candidate keys as all other sets are having redundant attributes that are not necessary for unique identification.

Tuesday 9 November 2021, 488 views

Next post: 10. ACID: Guaranteeing a DBMS against errors
Previous post: 8. Database normalization